¿"Partículas" que se relacionan vs relaciones que "particularizan"?

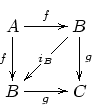Sobre un acontecimiento silencioso para el pensamiento (que puede usarse por ejemplo en ámbitos "educativos" (ámbitos que mal que nos pese, existen)).

1. En resumen...
2. En usando... materiales y usos...

1.- Un "acontecimiento silencioso" [1] para el "pensamiento" (que tiene que ver con las matemáticas, etc) aún no ha "traspasado" y lleva ya bastantes años "ocurriendo".

Aunque en principio parece haber muchas cosas con estas "características" por el mundo, como esto va de "fundamentos" podría ser que fuera de vuestra utilidad, así que lo comentamos.

Ya imaginarás que si unas "matemáticas" tan básicas como son los conceptos de conjuntos nos las pueden dar hasta en la educación infantil, el proceso de "comunicación inconsciente" en que a veces consiste ese tema de los fundamentos de las matemáticas no tiene por qué dejar de "evolucionar", por supuesto (aunque ya se sabe, "la escuela", con la "sociedad", es algo que puede o debería poder evolucionar más en general y de diversos modos, pero esa es "otra historia"...).

De hecho a lo que llegan de repente las matemáticas a mediados del siglo XX es a forzar definitiva y repentinamente una especie de "giro" (ese "poder de las palabras"...). Un giro que no ha transcendido, por supuesto, a la en cierto modo excesivamente "obsesionada" "educación-basada-en-elementos-de-conjuntos-y-partículas".

Básicamente dos matemáticos deciden la palabra "categoría" para hablar de un universo de relaciones -y objetos (y poco más). Pero la clave está en que se dan cuenta de que un enfoque que de mayor importancia al "morfismo", la flecha, la relación, es útil, muy profundo y fundamental.

Se establece entonces, con aquello de "categoría", un marco que pudiéramos llamar más "holista". Nos encontramos de repente con una clara posibilidad de hablar de cierta interdependencia entre "relaciones" e "interiores", entre "aparecer" y "ser".

Esto es, en principio, y como pensamiento inicial sobre todo esto, podríamos decir que un ser determinado, un objeto, "no sería nada" fuera de la categoría en la que se inscriba. Esto es, un ser lleva aparejado un "universo relacional" (por ejemplo, decir que tenemos "conjuntos", esto es, objetos que son "bolsas" de pelotas sin cohesión entre sí, nos obliga a no tener una libertad en cuanto al universo relacional donde inscribimos tales objetos: las aplicaciones entre los conjuntos, si las elegimos como nos las dieron en la escuela, no se pueden elegir de cualquier manera en este universo de relaciones entre "seres sin cohesión".).

O, partiendo a su vez desde la dimensión del "aparecer", de la de las meras relaciones, podemos por ejemplo pensar inicialmente cómo las restricciones que vayamos poniendo a un tal universo relacional -a sus flechas y sin mirar al interior/ser de los objetos- pueden o no dar cabida a varios tipos de ser/interior. Osea, podríamos decir que diferentes "lógicas relacionales" permiten diferentes "seres", ya que la lógica es una dimensión que atañe a este aparecer, a estas "relaciones".

De hecho uno de los "logros" de esta teorización fundamental es una mejor visualización "matemática" de cómo la verdad parcial no es algo accesorio, ni mucho menos, en matemáticas. La "verdad" depende de las
relaciones que rodean a un objeto particular en nuestra categoría, el cual -y si la categoría lo "admite"- se llama "objeto de valores de verdad" (que en la categoría de conjuntos es el "2", conjunto de dos elementos, sí/no; seguramente "el causante" de todas nuestras diatribas contra el "pensamiento binario", ya que como "seres inteligentes" y sin "cortapisas", en cierto modo ya "sabríamos" o tendríamos la capacidad de intuir teorías más avanzadas y esto de empezar la "lógica"/pensamiento
por un "sí/no" echa y ha "echado para" atrás a cualquiera (ya que de hecho es muy desagradable a veces, vaya)).

2.- Utilidad y materiales

Así que para terminar comentamos que puede ser útil para ti, o tus amig@s tener noticia de esto si es que no la tuvieras ya. Puede por ejemplo usarse para motivar "didácticas" de eso que dicen que dan bajo el nombre de "matemáticas" y que es a veces demasiado instrumental, o puede usarse en general para didáctica en cuanto al pensamiento en general.

Existe un libro que da cuenta de este tema apropiadamente, aunque desde la óptica de las "matemáticas puras", si bien la "línea de fuga" hacia mayores contactos con la "filosofía" e "interdisciplinariedades varias" la podemos ver reflejada en el título:

"Matemáticas conceptuales: una primera traducción a categorías". Lawvere $ Schanuel. Editado por siglo XXI en Méjico, pero encontrable en España y afortunadamente no muy caro, aunque por supuesto con "copyright".
(¡No tenemos comisión ni somos vendedores! ¡No vayáis a ser malpensados!)

De hecho la palabra 'filosofía' aparece en este texto donde se da de hecho una simple y posible descripción/definición de los cometidos de la filosofía, que, por cierto, es llamada también "ciencia" en el libro.

En esta página tengo unos pocos enlaces y comentarios relativos al libro. Y en general aquí tengo más textos introductorios -más o menos "locos"- aparte de algún que otro atisbo conceptual en la wiki o en los html, y algún que otro comienzo más formal... etc. Pero por ahora todo está bastante "iniciático" y las capacidades técnicas de comunicación debieran poderse aumentar, pero bueno.

Así que si da la casualidad de que te interesa o conoces a alguien interesado o que quiera interesarse me tienen vdes a su disposición para ayudar en lo que pudiera -y para que me ayuden claro.

Notas

[1] El filósofo francés Alain Badiou usa esas palabras hablando de este
tema en el libro también "recientemente" publicado: "Breve tratado de
ontología transitoria", Gedisa editorial. Por ejemplo.